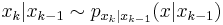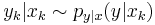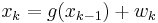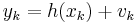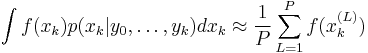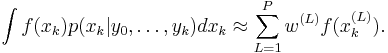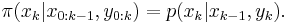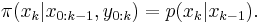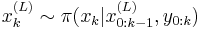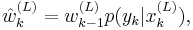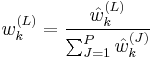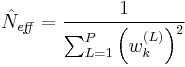Particle filter
In statistics, particle filters, also known as Sequential Monte Carlo methods (SMC), are sophisticated model estimation techniques based on simulation.[1] Particle filters have important applications in econometrics,[2] and in other fields.
Particle filters are usually used to estimate Bayesian models in which the latent variables are connected in a Markov chain — similar to a hidden Markov model (HMM), but typically where the state space of the latent variables is continuous rather than discrete, and not sufficiently restricted to make exact inference tractable (as, for example, in a linear dynamical system, where the state space of the latent variables is restricted to Gaussian distributions and hence exact inference can be done efficiently using a Kalman filter). In the context of HMMs and related models, "filtering" refers to determining the distribution of a latent variable at a specific time, given all observations up to that time; particle filters are so named because they allow for approximate "filtering" (in the sense just given) using a set of "particles" (differently-weighted samples of the distribution).
Particle filters are the sequential ("on-line") analogue of Markov chain Monte Carlo (MCMC) batch methods and are often similar to importance sampling methods. Well-designed particle filters can often be much faster than MCMC. They are often an alternative to the Extended Kalman filter (EKF) or Unscented Kalman filter (UKF) with the advantage that, with sufficient samples, they approach the Bayesian optimal estimate, so they can be made more accurate than either the EKF or UKF. However, when the simulated sample is not sufficiently large, they might suffer from sample impoverishment. The approaches can also be combined by using a version of the Kalman filter as a proposal distribution for the particle filter.
Contents |
Goal
The particle filter aims to estimate the sequence of hidden parameters, xk for k = 0,1,2,3,…, based only on the observed data yk for k = 0,1,2,3,…. All Bayesian estimates of xk follow from the posterior distribution p(xk | y0,y1,…,yk). In contrast, the MCMC or importance sampling approach would model the full posterior p(x0,x1,…,xk | y0,y1,…,yk).
Model
Particle methods assume 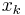 and the observations
and the observations 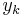 can be modeled in this form:
can be modeled in this form:
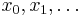 is a first order Markov process such that
is a first order Markov process such that
and with an initial distribution 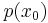 .
.
- The observations
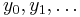 are conditionally independent provided that
are conditionally independent provided that 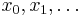 are known
are known
- In other words, each
 only depends on
only depends on 
One example form of this scenario is
where both 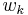 and
and 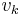 are mutually independent and identically distributed sequences with known probability density functions and
are mutually independent and identically distributed sequences with known probability density functions and 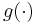 and
and 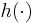 are known functions. These two equations can be viewed as state space equations and look similar to the state space equations for the Kalman filter. If the functions
are known functions. These two equations can be viewed as state space equations and look similar to the state space equations for the Kalman filter. If the functions 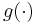 and
and 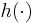 are linear, and if both
are linear, and if both 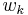 and
and 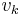 are Gaussian, the Kalman filter finds the exact Bayesian filtering distribution. If not, Kalman filter based methods are a first-order approximation (EKF) or a second-order approximation (UKF in general, but if probability distribution is Gaussian a third-order approximation is possible). Particle filters are also an approximation, but with enough particles they can be much more accurate.
are Gaussian, the Kalman filter finds the exact Bayesian filtering distribution. If not, Kalman filter based methods are a first-order approximation (EKF) or a second-order approximation (UKF in general, but if probability distribution is Gaussian a third-order approximation is possible). Particle filters are also an approximation, but with enough particles they can be much more accurate.
Monte Carlo approximation
Particle methods, like all sampling-based approaches (e.g., MCMC), generate a set of samples that approximate the filtering distribution 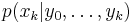 . So, with
. So, with  samples, expectations with respect to the filtering distribution are approximated by
samples, expectations with respect to the filtering distribution are approximated by
and  , in the usual way for Monte Carlo, can give all the moments etc. of the distribution up to some degree of approximation.
, in the usual way for Monte Carlo, can give all the moments etc. of the distribution up to some degree of approximation.
Sequential Importance Resampling (SIR)
Sequential importance resampling (SIR), the original particle filtering algorithm (Gordon et al. 1993), is a very commonly used particle filtering algorithm, which approximates the filtering distribution 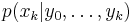 by a weighted set of P particles
by a weighted set of P particles
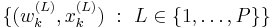 .
.
The importance weights 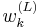 are approximations to the relative posterior probabilities (or densities) of the particles such that
are approximations to the relative posterior probabilities (or densities) of the particles such that 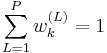 .
.
SIR is a sequential (i.e., recursive) version of importance sampling. As in importance sampling, the expectation of a function 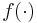 can be approximated as a weighted average
can be approximated as a weighted average
For a finite set of particles, the algorithm performance is dependent on the choice of the proposal distribution
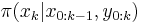 .
.
The optimal proposal distribution is given as the target distribution
However, the transition prior is often used as importance function, since it is easier to draw particles (or samples) and perform subsequent importance weight calculations:
Sequential Importance Resampling (SIR) filters with transition prior as importance function are commonly known as bootstrap filter and condensation algorithm.
Resampling is used to avoid the problem of degeneracy of the algorithm, that is, avoiding the situation that all but one of the importance weights are close to zero. The performance of the algorithm can be also affected by proper choice of resampling method. The stratified sampling proposed by Kitagawa (1996) is optimal in terms of variance.
A single step of sequential importance resampling is as follows:
- 1) For
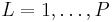 draw samples from the proposal distribution
draw samples from the proposal distribution
- 2) For
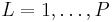 update the importance weights up to a normalizing constant:
update the importance weights up to a normalizing constant:
-
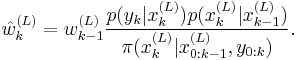
- Note that when we use the transition prior as the importance function,
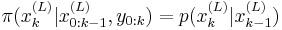 , this simplifies to the following :
, this simplifies to the following :
- 3) For
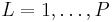 compute the normalized importance weights:
compute the normalized importance weights:
- 4) Compute an estimate of the effective number of particles as
- 5) If the effective number of particles is less than a given threshold
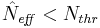 , then perform resampling:
, then perform resampling:
-
- a) Draw
 particles from the current particle set with probabilities proportional to their weights. Replace the current particle set with this new one.
particles from the current particle set with probabilities proportional to their weights. Replace the current particle set with this new one.
- a) Draw
-
- b) For
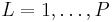 set
set 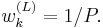
- b) For
The term Sampling Importance Resampling is also sometimes used when referring to SIR filters.
Sequential Importance Sampling (SIS)
- Is the same as Sequential Importance Resampling, but without the resampling stage.
"Direct version" algorithm
The "direct version" algorithm is rather simple (compared to other particle filtering algorithms) and it uses composition and rejection. To generate a single sample  at
at  from
from 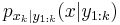 :
:
- 1) Set n=0 (This will count the number of particles generated so far)
- 2) Uniformly choose an index L from the range
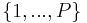
- 3) Generate a test
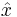 from the distribution
from the distribution 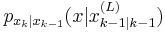
- 4) Generate the probability of
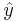 using
using 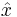 from
from 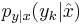 where
where 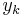 is the measured value
is the measured value
- 5) Generate another uniform u from
![[0, m_k]](/2012-wikipedia_en_all_nopic_01_2012/I/7bdc57b202e156c251b7dbf9529244bd.png)
- 6) Compare u and
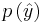
-
- 6a) If u is larger then repeat from step 2
-
- 6b) If u is smaller then save
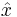 as
as 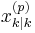 and increment n
and increment n
- 6b) If u is smaller then save
- 7) If n == P then quit
The goal is to generate P "particles" at  using only the particles from
using only the particles from 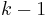 . This requires that a Markov equation can be written (and computed) to generate a
. This requires that a Markov equation can be written (and computed) to generate a 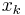 based only upon
based only upon 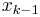 . This algorithm uses composition of the P particles from
. This algorithm uses composition of the P particles from 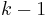 to generate a particle at
to generate a particle at  and repeats (steps 2-6) until P particles are generated at
and repeats (steps 2-6) until P particles are generated at  .
.
This can be more easily visualized if  is viewed as a two-dimensional array. One dimension is
is viewed as a two-dimensional array. One dimension is  and the other dimensions is the particle number. For example,
and the other dimensions is the particle number. For example, 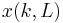 would be the Lth particle at
would be the Lth particle at  and can also be written
and can also be written 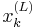 (as done above in the algorithm). Step 3 generates a potential
(as done above in the algorithm). Step 3 generates a potential 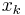 based on a randomly chosen particle (
based on a randomly chosen particle (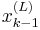 ) at time
) at time 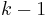 and rejects or accepts it in step 6. In other words, the
and rejects or accepts it in step 6. In other words, the 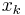 values are generated using the previously generated
values are generated using the previously generated 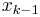 .
.
Other Particle Filters
- Auxiliary particle filter
- Gaussian particle filter
- Unscented particle filter
- Monte Carlo particle filter
- Gauss-Hermite particle filter
- Cost Reference particle filter
- Rao-Blackwellized particle filter
See also
References
- ^ Doucet, A.; De Freitas, N.; Gordon, N.J. (2001). Sequential Monte Carlo Methods in Practice. Springer.
- ^ Thomas Flury & Neil Shephard, 2008. "Bayesian inference based only on simulated likelihood: particle filter analysis of dynamic economic models," OFRC Working Papers Series 2008fe32, Oxford Financial Research Centre.
Bibliography
- Cappe, O.; Moulines, E.; Ryden, T. (2005). Inference in Hidden Markov Models. Springer.
- Liu, J. (2001). Monte Carlo strategies in Scientific Computing. Springer.
- Ristic, B.; Arulampalam, S.; Gordon, N. (2004). Beyond the Kalman Filter: Particle Filters for Tracking Applications. Artech House.
- Doucet, A.; Johansen, A.M.; (December 2008). "A tutorial on particle filtering and smoothing: fifteen years later". Technical report, Department of Statistics, University of British Columbia. http://www.cs.ubc.ca/%7Earnaud/doucet_johansen_tutorialPF.pdf.
- Doucet, A.; Godsill, S.; Andrieu, C.; (2000). "On sequential Monte Carlo sampling methods for Bayesian filtering". Statistics and Computing 10 (3): 197–208. doi:10.1023/A:1008935410038. http://www.springerlink.com/content/q6452k2x37357l3r/.
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T.; (2002). "A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking". IEEE Transactions on Signal Processing 50 (2): 174–188. doi:10.1109/78.978374. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=978374.
- Cappe, O.; Godsill, S.; Moulines, E.; (2007). "An overview of existing methods and recent advances in sequential Monte Carlo". Proceedings of IEEE 95 (5): 899. doi:10.1109/JPROC.2007.893250.
- Kitagawa, G. (1996). "Monte carlo filter and smoother for non-Gaussian nonlinear state space models". Journal of Computational and Graphical Statistics (Journal of Computational and Graphical Statistics, Vol. 5, No. 1) 5 (1): 1–25. doi:10.2307/1390750. JSTOR 1390750.
- Kotecha, J.H.; Djuric, P.; (2003). "Gaussian Particle filtering". IEEE Transactions Signal Processing 51 (10).
- Haug, A.J. (2005). "A Tutorial on Bayesian Estimation and Tracking Techniques Applicable to Nonlinear and Non-Gaussian Processes". The MITRE Corporation, USA, Tech. Rep., Feb. http://www.mitre-corporation.net/work/tech_papers/tech_papers_05/05_0211/05_0211.pdf. Retrieved 2008-05-06.
- Pitt, M.K.; Shephard, N. (1999). "Filtering Via Simulation: Auxiliary Particle Filters". Journal of the American Statistical Association (Journal of the American Statistical Association, Vol. 94, No. 446) 94 (446): 590–591. doi:10.2307/2670179. JSTOR 2670179. http://www.questia.com/PM.qst?a=o&se=gglsc&d=5002321997. Retrieved 2008-05-06.
- Gordon, N. J.; Salmond, D. J. and Smith, A. F. M. (1993). "Novel approach to nonlinear/non-Gaussian Bayesian state estimation". IEEE Proceedings F on Radar and Signal Processing 140 (2): 107–113. doi:10.1049/ip-f-2.1993.0015. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=210672. Retrieved 2009-09-19.
- Chen, Z. (2003). Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.107.7415&rep=rep1&type=pdf. Retrieved 2010-10-14.
External links
- Feynman-Kac models and interacting particle algorithms (a.k.a. Particle Filtering) Theoretical aspects and a list of application domains of particle filters
- Sequential Monte Carlo Methods (Particle Filtering) homepage on University of Cambridge
- Dieter Fox's MCL Animations
- Rob Hess' free software
- SMCTC: A Template Class for Implementing SMC algorithms in C++
- Tutorial on particle filtering with the MRPT C++ library, and a mobile robot localization video.
- Java applet on particle filtering
- An example of human tracking using Particle filters, c++ code is also available for download.